Detection of Duplicate Records in Large-scale Multi-tenant Platforms

Paul O'Grady

#PyConIE - 6th November 2016

ME:

Currently Data Scientist at ...

Twitter: @paul_ogrady

Overview

• Multi-Tenant Platforms
• Record Linkage Problem
• Cartesian Joins
• Locality Sensitive Hashing
• LSH tuning

Platform

Record Linkage Problem

• The task of finding records in a data set that refer to the same entity across different data sources

• Necessary when joining data sets based on entities that may or may not share a common identifier—canonical ID

• Common problem, e.g.:

  +----+------------+-------------+---------------------------------+
  | ID | First Name | Second Name | Address                         |
  +----+------------+-------------+---------------------------------+
  | 19 | G.         | Van Rossum  | PSF, 9450 SW Gemini Dr. ...     |
  +----+------------+-------------+---------------------------------+
  | 56 | Guido      | V. Rossum   | Python Software Foundation, ... |
  +----+------------+-------------+---------------------------------+
  

Multi-Tenant Platform

Records \(\equiv\) Products

• One platform, multiple (siloed) users may be selling the same products leading to duplicates
• Unique IDs may be unreliable, therefore we examine record content, i.e., product attributes
• Grouping duplicates under a canonical ID helps with:
  • Satisfying customer requests (Smart Logistics)
  • BI & ML insights (Smart Product Platform)
  • Cross-sectional insights (How products are bought)

Product Similarity

Product Similarity

• Record Linkage can be tackled using a notion of record similarity, where duplicates are close together
• Product attributes may have ordinal or categorical values, or contain images
• Ordinal Data: Vector space, cosine similarity, TFIDF
• Categorical Data: No order, cosine similarity will not work here
• Image Data: Feature Vectors, Deep Learning

We will be looking at Categorical Data

Product Space

Products exist in space/manifold

Product Space

Distances between products indicate similarity

Product Space

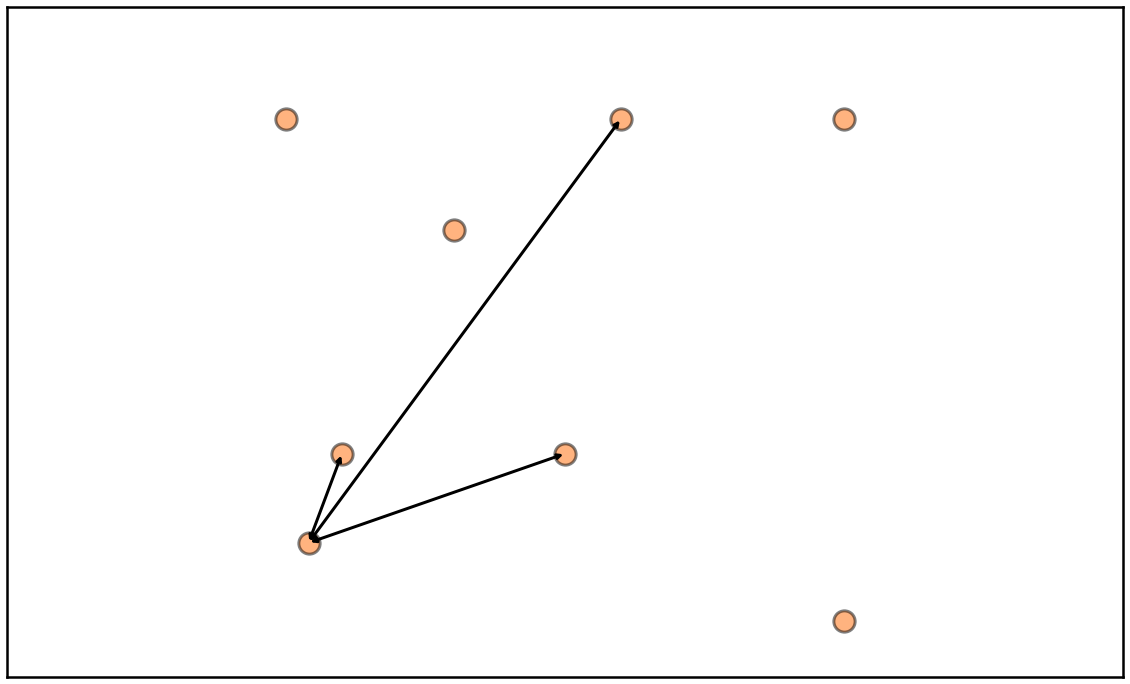
Product duplicates are products that are very similar

Cartesian Join

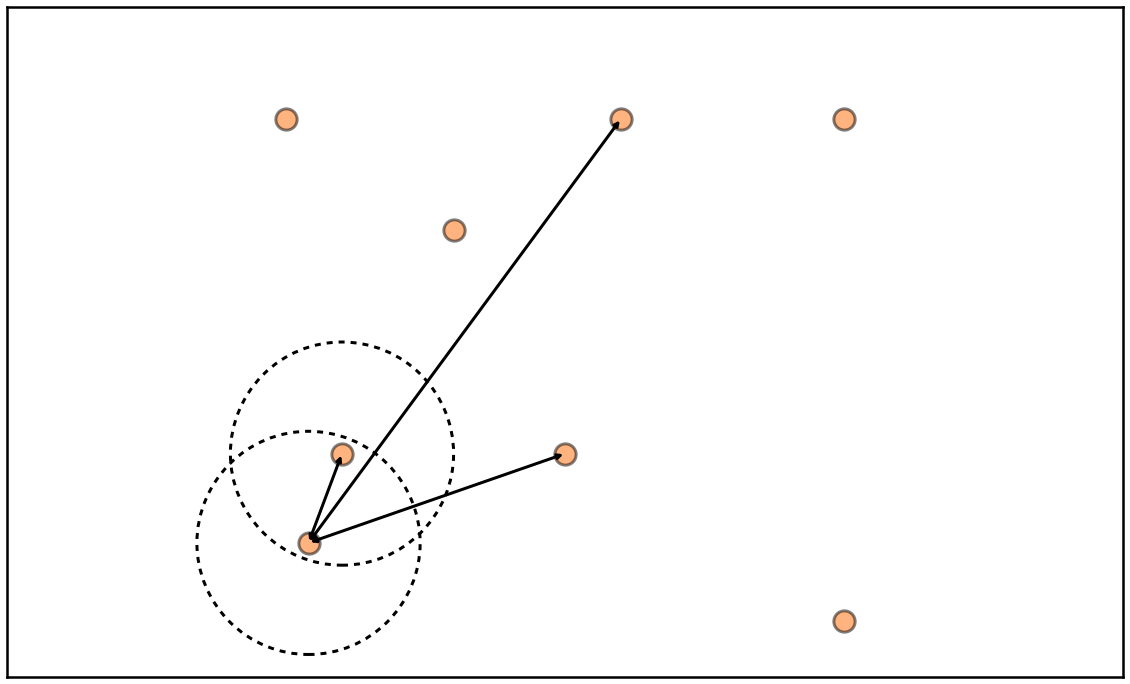
• Cartesian Join / All-pairs Join / Similarity Join \(O(n^2)\) *

  • A 10-fold increase in the input results in a 100-fold increase in the output—grows quadratically!

• Naive Solution:

  sim_scores = []
  for i, record_i  in enumerate(records):
      for j, record_j in enumerate(records):
          sim_scores.append(((i, j), sim(record_i, record_j)))
  

• Output:

  >>> sim_scores
  [((0, 0), 0), ((0, 1), 4), ((0, 2), 0), ((1, 0), -4), ((1, 1), 0),
   ((1, 2), -4), ((2, 0), 0), ((2, 1), 4), ((2, 2), 0)]
  

  ^* To be more correct our problem is O(n(n-1)/2)

Measuring Similarity

• How to calculate sim(record_i, record_j)?

• Composite Similarity Measure:

  Weighted combination of individual attribute similarity measures, \({f_i,\dots,f_N}\):

  \[\begin{split}S(p_i, p_j) & = w_1 f_1(a_{i1}, a_{j1}) + w_2 f_2(a_{i2}, a_{j2}) \\ & + \dots + w_N f_N(a_{iN}, a_{jN})\end{split}\]

  where \({a_i,\dots,a_N}\) are the product attributes, \({f_i,\dots,f_N}\) are their similarity measures and \({w_i,\dots,w_N}\) are the weighting in the model [1].

Composite Similarity Measure

• \(f_i\) we use Hamming Distance between attributes *

• \(w_i\) are learned from training data using an Averaged Perceptron, \(\hat y = \text{sign}(\mathbf{w_{avg}} \cdot \mathbf{x})\)

• Code:

  for t in range(T):
      for i in range(M):
          x = training_data[i,:] # f() applied in advance
          y = labels[i]
          dot_prod = float(w.dot(np.matrix(x).T))
          y_est = sgn(dot_prod)
          if y_est != y:
              w = w + (y * x)
          w_avg += w
  
   w_avg = w_avg / (T*M)
  

  ^* We use other categorical similarity measures that we do not discuss here

Hamming Distance

• The Hamming/Overlap distance between two records is the number of attributes in which they differ

  \[f_i(x, y) = H(x,y) = \sum_{i=1}^{N} \text{int}(x_i \neq y_i)\]

• Code:

  def hamming_distance(x, y):
      return sum(elx != ely for elx, ely in zip(x, y))
  

• Output:

  >>> x = "Foo Bar Baz Qux"; y = "Foo Bar Baz corge"
  >>> hamming_distance(x, y)
  1
  

Scaling Up

Scaling Up De-duplication

• Problem grows quadratically; quickly run into trouble as # of Products > 1M (499,999,500,000 comparisons)
• All-pairs similarity calculates all scores, misses no duplicates

Q: If we relax our requirements on missing duplicates can we use a trick?

A: Yes - Locality-Sensitive Hashing (LSH)

Locality-Sensitive Hashing

• LSH hashes input items so that similar items map to the same buckets with high probability [2]

• LSH differs from cryptography hash functions because it aims to maximize the probability of collisions

• Similarity is measured using the Jaccard Index

• LSH parameters:

  • \(r\): number of rows/hashes per band
  • \(b\): number of bands

  LSH is an exercise in tuning r & b for desired similarity & accuracy

Jaccard Index

• The Jaccard index is useful for comparing segments of text

  \[J(x,y) = {{|x \cap y|}\over{|x \cup y|}} = {{|x \cap y|}\over{|x| + |y| - |x \cap y|}}\]

• Code:

  def jaccard_index(x, y):
      return len(x.intersection(y)) / len(x.union(y))
  

• Example:

  >>> x = "Foo Bar Baz Qux"; y = "Qux Baz Bar Quux"
  >>> jaccard_index(set(x.split()), set(y.split()))
  0.6
  

Simple Hashing

• Simple hashing function that hashes \(x\) to \(N\) buckets:

  \[h_{a}(x) = (a x + 1) \, \text{mod} \, N\]

  where \(a\) is a random integer & \(N\) is a prime number (to avoid collisions)

• Code:

  class SimpleHash:
      def __init__(self, a, N, c=1):
          self.a = a; self.N = N; self.c = c
      def __call__(self, x):
          return (self.a * x + self.c)  % self.N
  

• Example:

  >>> hash_ = SimpleHash(a=5, N=7)
  >>> [hash_(i) for i in range(7)]
  [1, 6, 4, 2, 0, 5, 3]
  

Min-Hashing

• Convert large sets to short signatures, while preserving similarity

  \[Pr[h_\pi(p_1) = h_\pi (p_2)] = J(p_1, p_2);\]

  For a random permutation \(\pi\).

• Code:

  def min_hash(a, hash_func):
      perm_ind = [hash_func(x) for x in range(a.shape[0])]
      return np.ma.masked_array(perm_ind, np.logical_not(a)).min()
  

• Example:

  >>> record_elements = np.array([0, 0, 1, 1, 0, 1, 1] )
  >>> hash_ = simple_hash(a=5, N=7); [hash_(i) for i in range(7)]
  [1, 6, 4, 2, 0, 5, 3]
  >>> min_hash(record_elements, hash_)
  2
  

Min-Hashing

[3]

LSH Band Hashing

LSH Bucketing

LSH Duplicate Detection

• Depending on \(r\) & \(b\) documents in buckets can be considered duplicate candidates
• A subsequent exact comparison is performed on candidates to identify duplicates
  • Cartesian join on Candidates
  • Composite Similarity Measure
• We use LSH as a duplicate pre-filtering step, then follow with an exact comparison between candidates

System Tuning

Prob. of Two Products in Same Bucket?

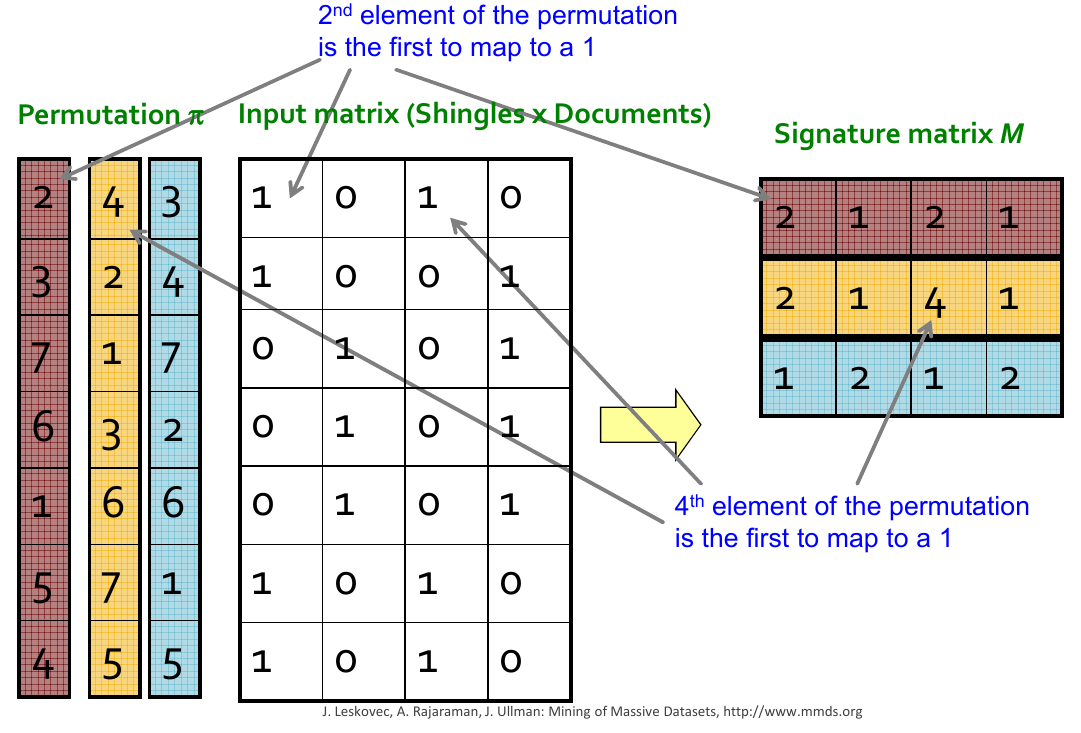
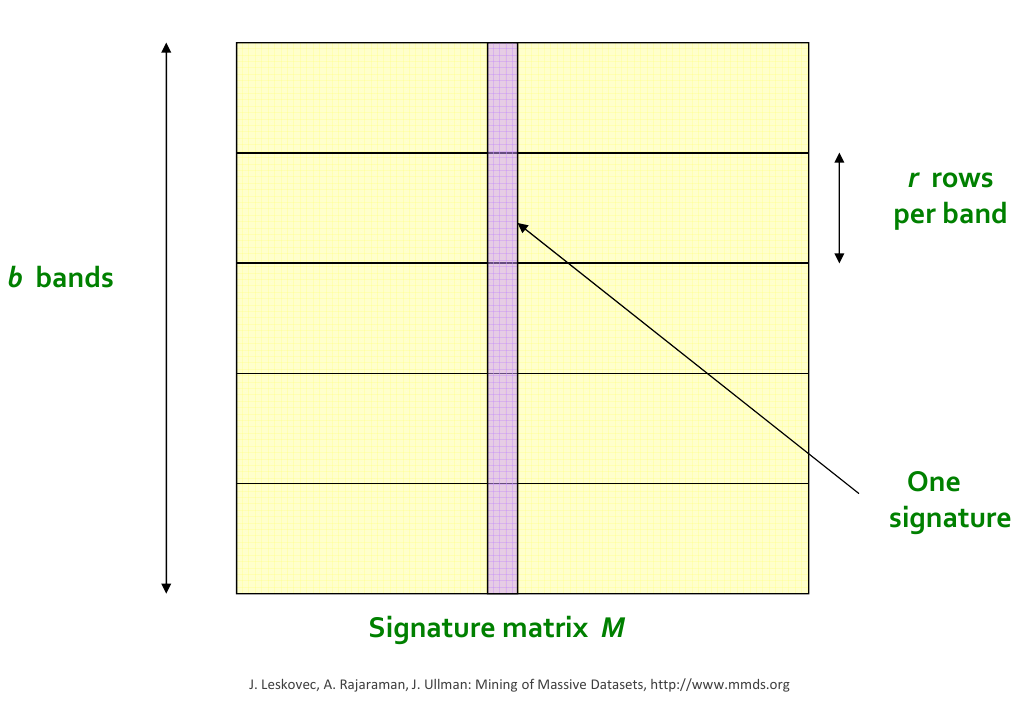
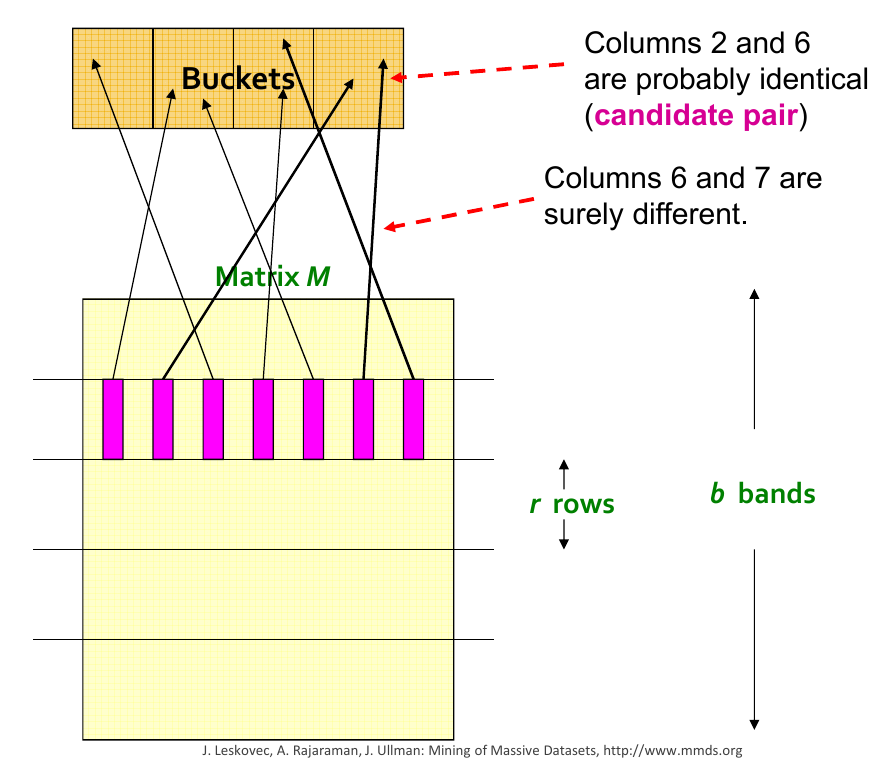
For s-similar products, where r is the number of rows and b is the number of bands

prob. that all rows in band equal, \(t^r\)

prob. that some row in band unequal, \(1 - t^r\)

prob. that no band identical, \((1 - t^r)^b\)

prob. that at least 1 band identical (s-curve),

LSH S-curve Tuning

Candidate-Pair Probability

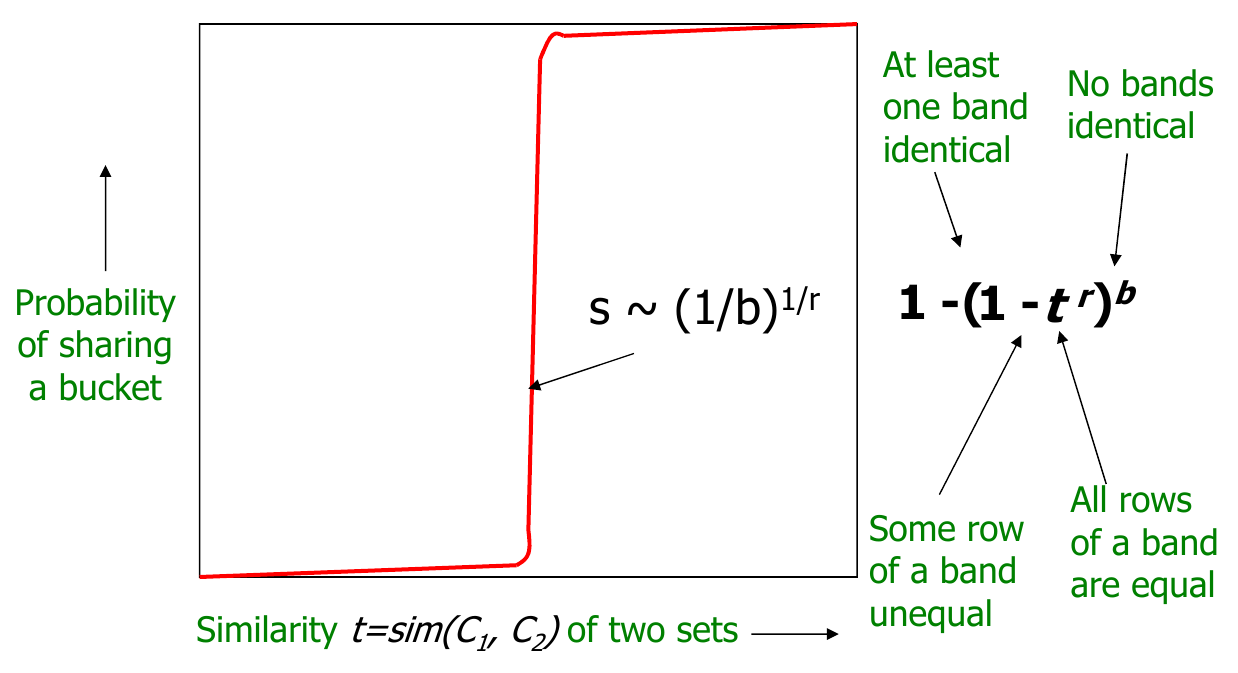
• LSH params: \(r=4\) & \(b=16\). Candidate Pair Probability:

  Similarity	Probability
  0.00	0.000000000
  0.10	0.001598801
  0.20	0.025295082
  0.30	0.122016723
  0.40	0.339616210
  0.50	0.643925870
  0.60	0.891481916
  0.70	0.987637591
  0.80	0.999782058
  0.90	0.999999962

Tuning r & b for specified s-similarity

• Optimise \(1 - (1 - t^r)^b\)

  • Reduce the area on the left of the s-curve threshold
  • Reduce the distance between the s-curve threshold and a specified target

• How to optimise?

  • Calc. max of derivative of candidate prob using sympy & scipy
  • Calc. definite integral for area left of threshold using sympy
  • Grid search: (r , b) for specified s-curve threshold & alpha.

Optimise With Reg.

def combine_outputs(x, alpha=1.0):
    area, thres_error = x
    return (1-alpha)*area + alpha*thres_error

def opt(max_hash_budget, target_s_threshold,
           alpha, use_s_thresh_approx, slices):

    # Setup function
    scurve = SCurveOpt(target_s_threshold, use_s_thresh_approx)
    func = lambda x : combine_outputs(scurve(x[0], x[1]), alpha) \
                        if x[0]*x[1] <= max_hash_budget else np.inf

    # Perform optimisation
    x0 , fval, grid, Jout = scipy.optimize.brute(
                    func, slices, full_output=True, finish=None)
    return x0 , fval, grid, Jout

Optimal LSH Params

Opt. args: [  5.  26.] # Rows, Bands

Questions?

References